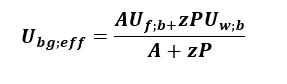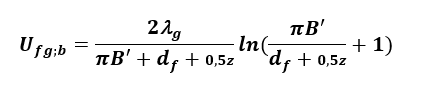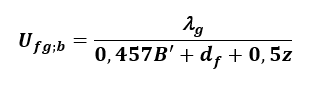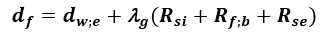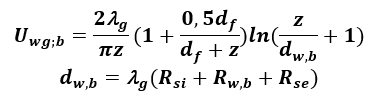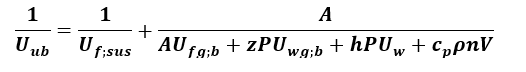Metodyka obliczeń cieplnych
Metodyka obliczeń cieplnych
1. Metodyka obliczeń cieplnych
Wartość współczynnika przenikania ciepła oblicza się wykorzystując metodę podaną w normie PN-EN ISO 6946:2017 [3]. Metoda ta pozwala na obliczanie oporu cieplnego i współczynnika przenikania ciepła płaskich komponentów budowlanych i elementów budynku za wyjątkiem drzwi, okien i innych komponentów szklonych i elementów, przez które odbywa się przenoszenie ciepła do gruntu np. podłóg na gruncie i ścian podziemnej części budynku.
Zasada metody obliczania podana w normie PN EN ISO 6946:2017 [3] polega na:
- określeniu oporu cieplnego każdej jednorodnej cieplnie części komponentu budowlanego,
- zsumowaniu tych poszczególnych oporów tak, aby uzyskać całkowity opór cieplny komponentu, łącznie (w miarę potrzeby) z oporami przejmowania ciepła na powierzchniach zewnętrznej i wewnętrznej.
Opory cieplne poszczególnych części oblicza się według normy PN ISO 6946: 2017 [3]. W większości przypadków przyjmuje się wartości oporów przejmowania ciepła na powierzchni podane w 6.8 PN ISO 6946: 2017 [3] W Załączniku C podano szczegółowe procedury dla powierzchni o niskiej emisyjności, określonych prędkości wiatru i powierzchni niepłaskich. W niniejszej Normie Międzynarodowej warstwy powietrza można rozpatrywać jako jednorodne cieplnie.
Opory warstw sumuje się następująco:
- w odniesieniu do komponentów składających się z warstw jednorodnych cieplnie, całkowity opór cieplny otrzymuje się według 6.7. ,a współczynnik przenikania ciepła według rozdziału 6.5 PN EN ISO 6946:2017 [3],
- w odniesieniu do komponentów z co najmniej jedną warstwą niejednorodną cieplnie, całkowity opór cieplny otrzymuje się według 6.7.2 PN EN ISO 6946:2017 [3],
- w odniesieniu do komponentów z warstwą o zmiennej grubości, współczynnik przenikania ciepła i/lub całkowity opór cieplny oblicza się według załącznika E normy PN EN ISO 6946:2017 [3].
Na koniec uwzględnia się, w miarę potrzeby, poprawki do współczynnika przenikania ciepła zgodnie z Załącznikiem F, w celu uwzględnienia efektów pustek w izolacji, łączników mechanicznych przechodzących przez warstwę izolacji i opadów na dachy odwrócone.
Opór cieplny warstw jednorodnych
Całkowity opór cieplny przegrody budowlanej opisuje wzór [3]:
(1)
Rtot = Rsi + R1 + R2 + … + Rn + Rse
gdzie:
- Rsi - opór przejmowania ciepła na powierzchni wewnętrznej przegrody [(m2∙K)/W],
- Rse - opór przejmowania ciepła na powierzchni zewnętrznej przegrody [(m2∙K)/W],
- R1, R2, …, Rn - obliczeniowe opory cieplne każdej warstwy [(m2∙K)/W].
|
Opór przejmowania ciepła [m2∙K/W] |
Kierunek strumienia ciepła |
||
|
w górę |
poziomy |
w dół |
|
|
Rsi |
0,10 |
0,13 |
0,17 |
|
Rse |
0,04 |
0,04 |
0,04 |
Znając całkowity opór cieplny analizowanej przegrody, obliczamy jej współczynnik przenikania ciepła U [W/(m2∙K)] [3]:
(2)
Opór cieplny warstw powietrza
Rodzaj i grubość szczeliny powietrznej dobiera projektant pamiętając, że do obliczeń cieplnych przyjęto rozróżniać trzy rodzaje szczelin wykształconych na etapie projektowania i montażu warstwy elewacyjnej zgodnie z PN EN ISO 6946:2017 [3]:
- dobrze wentylowaną,
- słabo wentylowaną,
- niewentylowaną szczelinę powietrzną.
Dobrze wentylowaną warstwą powietrza jest taka, w której pole powierzchni otworów między warstwą powietrza a otoczeniem zewnętrznym przekracza:
– 1500 mm2 na m długości – w przypadku pionowych warstw powietrza,
– 1500 mm2 na m2 powierzchni – w przypadku poziomych warstw powietrza.
Słabo wentylowaną warstwą powietrza jest taka, w której jest możliwy ograniczony przepływ powietrza zewnętrznego przez otwory o polu powierzchni zawartym
w następujących granicach:
– > 500 mm2, ale ≤ 1500 mm2 na m długości – w przypadku pionowych warstw powietrza,
– > 500 mm2, ale ≤ 1500 mm2 na m2 powierzchni – w przypadku poziomych warstw powietrza.
Niewentylowana warstwa powietrza : warstwę powietrza bez izolacji cieplnej między nią a środowiskiem zewnętrznym, z małymi otworami do środowiska zewnętrznego, też można uważać za niewentylowaną, jeżeli otwory te nie są przewidziane do stałego przepływu powietrza przez warstwę i pole ich powierzchni nie przekracza:
– 500 mm2 na m długości – w przypadku pionowych warstw powietrza,
– 500 mm2 na m2 powierzchni – w przypadku poziomych warstw powietrza
Opór cieplny przegród z warstwami jednorodnymi i niejednorodnym
Opór cieplny przegrody, zawierającej w swojej budowie warstwy jednorodne i niejednorodne (np. dach drewniany z dociepleniem pomiędzy krokwiami), oblicza się metodą uproszczoną zgodnie z normą [3]. W metodzie tej dokonuje się myślowego podziału przegrody płaszczyznami adiabatycznymi (prostopadłymi do powierzchni przegrody) i izotermicznymi (równoległymi do powierzchni przegrody). W wyniku takiego podziału uzyskuje się tzw. kres górny (płaszczyzny adiabatyczne) oraz kres dolny (płaszczyzny izotermiczne) całkowitego oporu cieplnego, wyznaczanego zgodnie z poniższym wyrażeniem [3]:
(3)
gdzie:
- Rtot,upper - kres górny całkowitego oporu cieplnego [(m2∙K)/W],
- Rtot;lower - kres dolny całkowitego oporu cieplnego [(m2∙K)/W].
W wyniku zastosowania metody uproszczonej, analizowany komponent zostaje podzielony na warstwy i wycinki. Każdemu wycinkowi przegrody odpowiada względne pole powierzchni. Suma względnych pół powierzchni wszystkich wycinków komponentu jest równa jedności [3]:
(4)
gdzie:
- fa, fb, …, fq – względne pola powierzchni każdego wycinka danej przegrody [-].
Kres górny całkowitego oporu cieplnego (przy założeniu, że wszystkie płaszczyzny prostopadłe do powierzchni analizowanej przegrody są adiabatyczne) wyznacza się według poniższego wyrażenia [3]:
(5)
gdzie:
- Rtot,a, Rtot,b, …, Rtot,q – całkowite opory cieplne każdego wycinka, [m2∙K/W].
Kres dolny całkowitego oporu cieplnego (przy założeniu, że wszystkie równoległe powierzchnie przegrody są izotermiczne) wyraża się następującym wzorem [3]:
(6)
Przy wyznaczaniu kresu dolnego, należy obliczyć równoważny opór cieplny Rj każdej warstwy niejednorodnej [3]:
(7)
gdzie:
- Raj, Rbj, …, Rqj – opory cieplne wycinków, budujących j-tą warstwę niejednorodną w danym komponencie [m2∙K/W].
Przy wyznaczaniu współczynnika przenikania ciepła przegrody wymagane jest uwzględnienie trzech poprawek, określonych w PN EN ISO 6946:2017 [3]. Wyróżnia się poprawkę z uwagi na:
- pustki powietrzne w warstwie izolacji,
- łączniki mechaniczne przebijające warstwę izolacyjną,
- zastosowanie dachu o odwróconym układzie warstw.
Poprawiony współczynnik przenikania ciepła, skorygowany o wyżej wymienione poprawki, oblicza się z następującego wzoru [3]:
(8)
Uc = U + ΔU
(9)
ΔU = ΔUg + ΔUg + ΔUr
gdzie:
- ΔUg - poprawka z uwagi na pustki powietrzne [W/(m2∙K)],
- ΔUf - poprawka z uwagi na łączniki mechaniczne [W/(m2∙K)],
- ΔUr - poprawka z uwagi na dach o odwróconym układzie warstw [W/(m2∙K)].
Poprawka z uwagi na pustki powietrzne
Zgodnie z normą [3], pustkami powietrznymi określa się przestrzenie powietrzne w izolacji termicznej przegrody lub między izolacją termiczną i przylegającą konstrukcją. Wyróżnia się dwie zasadnicze kategorie pustek powietrznych:
- szczeliny między arkuszami izolacyjnymi, płytami lub matami, lub między izolacją
i elementami konstrukcji, w kierunku strumienia ciepła, - wnęki w izolacji lub między izolacją i konstrukcją, prostopadle do kierunku strumienia ciepła.
Poprawkę ΔUg wyznacza się z poniższego wzoru [3]:
(10)
gdzie:
- R1 - opór cieplny warstwy zawierającej szczeliny [(m2∙K)/W],
- Rtot - całkowity opór cieplny komponentu z pominięciem mostków cieplnych [m2∙K/W],
- ΔU” - wartość przyjmowana zgodnie z tab. F.1 PN EN ISO 6946:2017 [3] [W/(m2∙K)].
|
Poziom |
Opis |
ΔU” [W/(m2∙K)] |
|
0 |
Brak pustek powietrznych w obrębie izolacji lub gdy występują tylko mniejsze pustki powietrzne, które nie mają znaczącego efektu na współczynnik przenikania ciepła. |
0,00 |
|
1 |
Pustki powietrzne przechodzące od ciepłej do zimnej strony izolacji, ale nie powodujące cyrkulacji powietrza między ciepłą i zimną stroną izolacji. |
0,01 |
|
2 |
Pustki powietrzne przechodzące od ciepłej do zimnej strony izolacji, łącznie z wnękami powodującymi swobodną cyrkulację powietrza między ciepłą i zimną stroną izolacji. |
0,04 |
Poprawka z uwagi na łączniki mechaniczne
Poprawkę do współczynnika U, z uwagi na łączniki mechaniczne, oblicza się jedną z dwóch procedur:
- obliczeniem szczegółowym,
- procedurą przybliżoną.
Wzór w obliczeniu szczegółowym jest następujący [3]:
(11)
gdzie:
- nf - liczba łączników na 1 m2,
- χ - punktowy współczynnik przenikania ciepła [W/K].
W procedurze przybliżonej poprawkę wyznacza się z poniższej zależności [3]:
(12)
gdzie:
- α = 0,8 (jeśli łącznik całkowicie przebija warstwę izolacji termicznej),
- α = 0,8 d1/d0 (w przypadku łącznika wpuszczanego),
- λf - współczynnik przewodzenia ciepła łącznika [W/(m∙K)],
- Af - pole przekroju poprzecznego jednego łącznika [m2],
- d0 - grubość warstwy izolacji zawierającej łącznik [m],
- d1 - długość łącznika, który przebija warstwę izolacyjną [m],
- R1 - opór cieplny warstwy izolacji przebijanej przez łączniki [(m2∙K)/W],
- Rtot- całkowity opór cieplny komponentu z pominięciem jakichkolwiek mostków cieplnych [m2∙K/W].
Poprawka z uwagi na dach o odwróconym układzie warstw
Poprawkę, wynikającą z przepływu wody między izolacją i membraną wodochronną, określa się z następującej zależności [3]:
(13)
gdzie:
- p - średnia wartość opadów atmosferycznych podczas sezonu ogrzewczego, na podstawie danych odpowiednich dla lokalizacji lub podana przez przepisy lokalne, regionalne czy krajowe lub inne dokumenty krajowe czy normy [mm/dzień],
- f - czynnik deszczowy podający frakcję p dochodzącą do membrany wodochronnej [-],
- x - czynnik zwiększenia strat ciepła spowodowanych przez wodę deszczową wpływającą na membranę [W∙dzień/(m2∙K∙mm)],
- R1 - opór cieplny warstwy izolacji powyżej membrany wodochronnej [m2∙K/W],
- Rtot - całkowity opór cieplny konstrukcji przed zastosowaniem poprawki [(m2∙K)/W].
2. Metodyka obliczeń cieplnych dla podłóg
Przenikanie ciepła przez przegrody pełne rozpatrujemy z zasady jako zadanie ustalonego, jednowymiarowego przewodzenia ciepła. Problem komplikuje się znacznie w przypadku przegród pełnych stykających się z gruntem: obliczanie strat ciepła do budynku przez grunt to złożone zadanie przewodzenia ciepła, w ogólności trójwymiarowe i niestacjonarne. Algorytm opisujący strumień ciepła przenoszony do gruntu przedstawiony został w normie PN EN ISO 13370:2017 [11]. Zakres tej normy obejmuje nie tylko przepływ ciepła z budynku ogrzewanego do gruntu; w załącznikach do tej normy rozpatruje się też inne zagadnienia m.in. podłogi chłodni i sztucznych lodowisk, podłogi z systemem ogrzewania i wpływ filtracji wody w gruncie.
Zjawisko wymiany ciepła między budynkiem i gruntem ma charakter przestrzenny; można jednak wprowadzić pewne uproszczenia, pomijając rzeczywisty kształt budynku, a wynikające z faktu, że największa wartość gęstości strumienia cieplnego następuje przy styku ze ścianą zewnętrzną i maleje w miarę oddalania się od ściany. W normie przyjęto koncepcję, zastąpienia rzeczywistego kształtu podłogi na gruncie figurą o obwodzie P i polu powierzchni A, zgodnymi z danymi rzeczywistego rzutu podłogi. Wprowadzono pojęcie wymiaru charakterystycznego PN EN ISO 13370:2017 [11]:
(14)
gdzie:
A-całkowite pole powierzchni podogi na gruncie [m2]
P – całkowity obwód budynku [m]
W przypadku podziemi B’ oblicza się z powierzchni i obwodu podłogi podziemia, nie uwzględniając jego ścian.
W normie przedstawiono procedury obliczeniowe w zakresie następujących przypadków:
- Podłoga typu płyta na gruncie,
- Podłoga podniesiona,
- Budynek z podziemiem ogrzewanym.
Płyta na gruncie: nieizolowana lub izolowana na całej powierzchni
Rys. 1. Płyta na gruncie (1- płyta podłogi, 2 – grunt) PN EN ISO 13370:2017 [11]
- płyta na gruncie – wszelkie podłogi składające się z płyty w kontakcie z gruntem na całej ich powierzchni oraz usytuowane na poziomie zewnętrznej powierzchni gruntu lub blisko niej, np. podłoga w budynku niepodpiwniczonym;
- płyty na gruncie mogą być nieizolowane lub równomiernie izolowane na całej powierzchni niezależnie od miejsca umieszczenia izolacji (powyżej, poniżej lub wewnątrz płyty);
Współczynnik przenikania ciepła zależy od wymiaru charakterystycznego podłogi B’ i całkowitej grubości równoważnej df PN EN ISO 13370:2017 [11].
(15)
gdzie:
λg – współczynnik przewodzenia ciepła gruntu, podane PN EN ISO 13370:2017 [11] [W/mK]
Rf,sog – opór cieplny podłogi [(m2K)/W], (opór cieplny płyt z ciężkiego betonu i cienkich wykładzin podłogowych można pominąć),
dw;e – grubość ścian zewnętrznych [m].
|
Rodzaj gruntu |
Współczynnik przewodzenia ciepła λ |
|
glina lub ił
|
1,50 |
|
piasek lub żwir
|
2,00 |
|
skała jednorodna
|
3,50 |
Wartość współczynnika przenikania ciepła U podłogi typu płyta na gruncie należy wyznaczać według niżej podanych wzorów, w zależności od tego czy można je uznać jako nieizolowane lub izolowane średnio, gdy df < B’, względnie jako podłogi dobrze izolowanej, gdy df ≥ B’
- podłogi nieizolowane lub izolowane średnio df< B’ PN EN ISO 13370:2017 [11]:
(16)
- podłogi dobrze izolowane df≥ B’ PN EN ISO 13370:2017 [11]:
(17)
Podłoga na gruncie typu płyta z izolacją krawędziową
Odmianami podłóg typu płyta na gruncie są podłogi z poziomą lub pionową izolacją krawędziową. Dla takich rodzajów podłóg współczynnik przenikania ciepła wyznaczać można z zależności PN EN ISO 13370:2017 [11]:
(18)
gdzie:
Ufg;sog;0 – współczynnik przenikania ciepła podłogi bez izolacji krawędziowej wyznaczony z zależności podanych powyżej [W/m2K],
ψg;ed – liniowy współczynnik przenikania ciepła związany z występowaniem izolacji krawędziowej wyznaczany w zależności od rodzaju izolacji krawędziowej (pozioma lub pionowa) [W/mK].
Liniowy współczynnik przenikania ciepła dla podłó g na gruncie typu płyta z poziomą izolacją krawędziową
Przypadek dotyczy podłóg, w których wzdłuż ścian zewnętrznych przewiduje się wykonanie poziomej izolacji cieplnej o szerokości D i grubości dn oraz oddzielenie podkładu pod posadzkę od ścian zewnętrznych pionowym paskiem materiału termoizolacyjnego o grubości identycznej jak w posadzce.
Rys. 2. Schemat poziomej izolacji krawędziowej (1- płyta podłogi, 2- izolacja pozioma, 3- ściana fundamentowa) PN EN ISO 13370:2017 [11]
Liniowy współczynnik przenikania ciepła związany z występowaniem izolacji krawędziowej ψg;ed można wyznaczyć z poniższej zależności PN EN ISO 13370:2017 [11]:
(19)
(20)
gdzie:
Rn – opór cieplny izolacji krawędziowej [m2K/W],
dn – grubość izolacji krawędziowej [m].
Liniowy współczynnik przenikania ciepła dla podłóg z pionową izolacją krawędziową lub ze ścianą fundamentową o małej gęstości
Rys. 3.Schemat pionowej izolacji krawędziowej ( 1 -ściana fundamentowa, 2- płyta podłogi, 3- izolacja pozioma) PN EN ISO 13370:2017 [11]
Przypadek dotyczy budynków, w których przewiduje się umieszczenie izolacji pionowej poniżej gruntu wzdłuż obwodu podłogi o grubości dn na głębokość D i do fundamentów z materiałów o współczynniku przewodzenia ciepła mniejszym niż gruntu oraz ścian fundamentowych o małej gęstości z λn < λg.
Liniowy współczynnik przenikania ciepła związany z występowaniem izolacji krawędziowej ψw;f można wyznaczyć z poniższej zależności PN EN ISO 13370:2017 [11]:
(21)
gdzie D – szerokość pionowej izolacji krawędziowej poniżej poziomu gruntu.
Podłoga podniesiona
Współczynnik przenikania ciepła podłogi podniesionej w stosunku do poziomu przyległego terenu o wysokość h z przestrzenią podpodłogową wentylowaną naturalnie należy wyznaczać z zależności PN EN ISO 13370:2017 [11]
(22)
gdzie:
Uf;sus – współczynnik przenikania ciepła podniesionej części podłogi (między środowiskiem wewnętrznym i przestrzenią podpodłogową) obliczany wg PN EN ISO 6946:2017 [3] [W/m2K],
Ug – współczynnik przenikania ciepła do gruntu z przestrzeni podpodłogowej [W/m2K],
(23)
Ux – ekwiwalentny współczynnik przenikania ciepła między przestrzenią podpodłogową i środowiskiem zewnętrznym [W/m2K],
(24)
gdzie:
h – wysokość górnej powierzchni podłogi podniesionej powyżej zewnętrznego poziomu gruntu [m],
Uw – współczynnik przenikania ciepła ściany przestrzeni podpodłogowej obliczony według normy PN EN ISO 6946:2017 [W/(m2·K)],
ε – pole powierzchni otworów wentylacyjnych przypadające na długość obwodu przestrzeni podpodłogowej [m2/m],
ν – średnia prędkość wiatru na wysokości 10 m [m/s],
fw – czynnik osłaniania przed wiatrem: osłonięte (centrum miasta) – 0,02, średnioosłonięte (przedmieścia) – 0,05, wyeksponowane (obszar wiejski) – 0,10.
Podłoga podziemi ogrzewanych
Rys. 5. Schemat budynku z podziemiem ogrzewanym (1- grunt) PN EN ISO 13370:2017 [11]
Efektywny współczynnik przenikania ciepła U’ dla całego podziemia ogrzewanego, zagłębionego w stosunku do poziomu terenu na głębokość z, w kontakcie z gruntem wyznacza się z zależności PN EN ISO 13370:2017 [11]:
(25)
gdzie:
Ubg;eff– współczynnik przenikania ciepła całego podziemia [W/m2K],
z – głębokość mierzona od poziomu terenu do poziomu posadzki podłogi [m],
Współczynnik przenikania ciepła podłogi Ubg;eff można wyznaczyć z poniższych zależności:
- podłogi nieizolowane lub średnio izolowane, df + 0,5z < B’
(26)
- podłogi dobrze izolowane, df + 0,5z ≥ B’
(27)
gdzie
Współczynnik przenikania ciepła dla ściany stykającej się z gruntem Ubw można wyznaczyć z zależności PN EN ISO 13370:2017 [11]:
(28)
Podziemie nieogrzewane
Dla podziemi nieogrzewanych wentylowanych powietrzem zewnętrzny współczynnik przenikania ciepła U między ośrodkiem zewnętrznym i wewnętrznym wyznaczać można z zależności PN EN ISO 13370:2017 [11]:
(29)
w której:
Uf;sus – współczynnik przenikania podłogi między środowiskiem wewnętrznym i podziemiem (strop nad piwnicą) wyznaczany według PN EN ISO 6946:2017 [3] [W/m2K],
Ufg;b, Uwg;b – współczynniki przenikania ciepła odpowiednio podłogi lub ściany poniżej poziomu gruntu wyznaczane z zależności jak dla podziemi ogrzewanych [W/m2K],
Uw – współczynnik przenikania ciepła ścian podziemia powyżej poziomu terenu wyznaczany według normy PN EN ISO 6946:2017 [3] [W/m2K],
h – wysokość górnej powierzchni podłogi nad podziemiem powyżej zewnętrznego poziomu gruntu [m],
cp- ciepło właściwe [Wh/(kgK)],
r- gęstość powietrza [kg/m3],
n – krotność wentylacji podziemia (liczba wymian na godzinę), którą w przypadku braku dokładnych danych można przyjąć równą n = 0,3 wymian na godzinę,
V – objętość powietrza w podziemiu.
Obliczeniowe wartości współczynników przenikania ciepła przegród stykających się z gruntem, czyli przegród poniżej posadzki parteru, należy wyznaczać według normy PN-EN ISO 13370:2017 [11]. Trzeba podkreślić, że metodyka zamieszczona w tej normie różni się od zasad podanych w normie PN-EN 12831:2006 [10] wykorzystywanej przy sporządzaniu charakterystyk i świadectw energetycznych budynków.
Według normy EN 12831:2006 [10] równoważny współczynnik przenikania ciepła Uequiv,bf elementu budynku (ściany i podłogi stykające się z gruntem) odczytuje się z podanych wykresów lub tablic, przy założeniu, że przewodność cieplna gruntu wynosi 2,0 W/(m²·K).
Na podstawie wykresu, znając wartość współczynnika przenikania ciepła podłogi oraz wartość charakterystycznego parametru B’, można wyznaczyć wartość Uequiv,bf.
Wartość równoważnego współczynnika przenikania ciepła Uequiv,bf rośnie wraz ze wzrostem wartości współczynnika przenikania ciepła Upodłogi i jednocześnie rośnie wraz ze zmniejszaniem się wartości parametru B’.




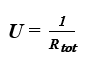
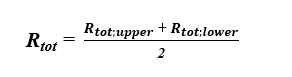
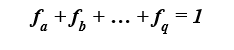
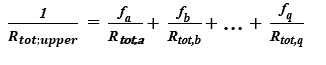
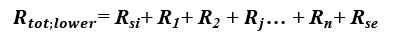
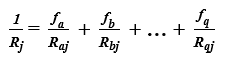
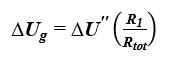
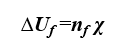
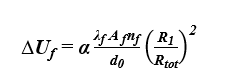
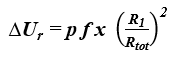
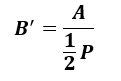
![Rys. 1. Płyta na gruncie (1- płyta podłogi, 2 – grunt) PN EN ISO 13370:2017 <a href="/konstrukcje-drewniane/termoizolacja/wybrane-akty-prawne-normy-literatura/#note-11" target="_blank">[11]</a>](/media/cache/full/781b1431cbbb4757b22db6207c18960c.PNG)
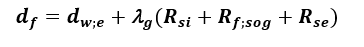
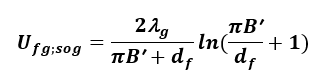
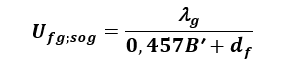
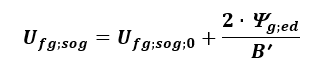
![Rys. 2. Schemat poziomej izolacji krawędziowej (1- płyta podłogi, 2- izolacja pozioma, 3- ściana fundamentowa) PN EN ISO 13370:2017 <a href="/konstrukcje-drewniane/termoizolacja/wybrane-akty-prawne-normy-literatura/#note-11" target="_blank">[11]</a>](/media/cache/full/8a42a090f4f9322e0220e13617ebc81e.PNG)
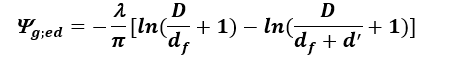
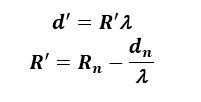
![Rys. 3.Schemat pionowej izolacji krawędziowej ( 1 -ściana fundamentowa, 2- płyta podłogi, 3- izolacja pozioma) PN EN ISO 13370:2017 <a href="/konstrukcje-drewniane/termoizolacja/wybrane-akty-prawne-normy-literatura/#note-11" target="_blank">[11]</a>](/media/cache/full/496fabbf511f16d6de9cbf9ad1dd73a4.PNG)
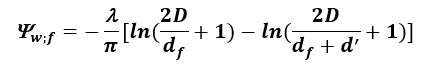
![Rys.4.Schemat podłogi podniesionej (1-grunt) [PN EN ISO 13370:2017]](/media/cache/full/b58f070e2ba5da78e1d910bf7164340e.PNG)
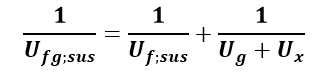
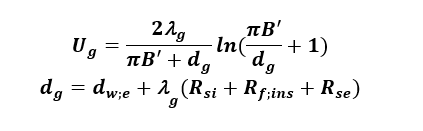
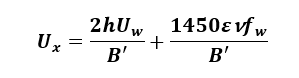
![Rys. 5. Schemat budynku z podziemiem ogrzewanym (1- grunt) PN EN ISO 13370:2017 <a href="/konstrukcje-drewniane/termoizolacja/wybrane-akty-prawne-normy-literatura/#note-11" target="_blank">[11]</a>](/media/cache/full/16e023a2223edc7bceac637b2a7375dd.PNG)