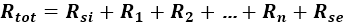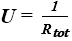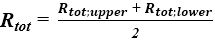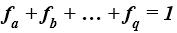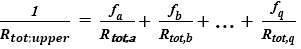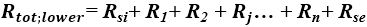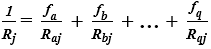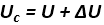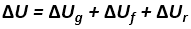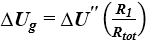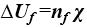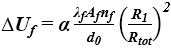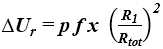Metodyka obliczeń cieplnych

Wartość współczynnika przenikania ciepła oblicza się wykorzystując metodę podaną w normie PN-EN ISO 6946:2017 [3]. Metoda ta pozwala na obliczanie oporu cieplnego i współczynnika przenikania ciepła płaskich komponentów budowlanych i elementów budynku za wyjątkiem drzwi, okien i innych komponentów szklonych i elementów, przez które odbywa się przenoszenie ciepła do gruntu np. podłóg na gruncie i ścian podziemnej części budynku.
 

Zasada metody obliczania podana w normie PN EN ISO 6946:2017 polega [3] na:

• określeniu oporu cieplnego każdej jednorodnej cieplnie części komponentu budowlanego,
• zsumowaniu tych poszczególnych oporów tak, aby uzyskać całkowity opór cieplny komponentu, łącznie (w miarę potrzeby) z oporami przejmowania ciepła na powierzchniach zewnętrznej i wewnętrznej.

Opory cieplne poszczególnych części oblicza się według normy PN EN ISO 6946:2017 [3] . W większości przypadków przyjmuje się wartości oporów przejmowania ciepła na powierzchni podane w 6.8 PN ISO 6946: 2017 [3] W Załączniku C podano szczegółowe procedury dla powierzchni o niskiej emisyjności, określonych prędkości wiatru i powierzchni niepłaskich. W niniejszej Normie Międzynarodowej warstwy powietrza można rozpatrywać jako jednorodne cieplnie.

Opory warstw sumuje się następująco:

• w odniesieniu do komponentów składających się z warstw jednorodnych cieplnie, całkowity opór cieplny otrzymuje się według 6.7. ,a współczynnik przenikania ciepła według rozdziału 6.5 PN EN ISO 6946:2017 [3] ,
• w odniesieniu do komponentów z co najmniej jedną warstwą niejednorodną cieplnie, całkowity opór cieplny otrzymuje się według 6.7.2 PN EN ISO 6946:2017 [3],
• w odniesieniu do komponentów z warstwą o zmiennej grubości, współczynnik przenikania ciepła i/lub całkowity opór cieplny oblicza się według załącznika E normy PN EN ISO 6946:2017 [3] ,

Na koniec uwzględnia się, w miarę potrzeby, poprawki do współczynnika przenikania ciepła zgodnie z Załącznikiem F, w celu uwzględnienia efektów pustek w izolacji, łączników mechanicznych przechodzących przez warstwę izolacji i opadów na dachy odwrócone.
 

Opór cieplny warstw jednorodnych

Całkowity opór cieplny przegrody budowlanej opisuje wzór  [3]

(1)

gdzie:

• R_si - opór przejmowania ciepła na powierzchni wewnętrznej przegrody [(m²∙K)/W],
• R_se - opór przejmowania ciepła na powierzchni zewnętrznej przegrody [(m²∙K)/W],
• R_1, R₂, …, R_n - obliczeniowe opory cieplne każdej warstwy [(m²∙K)/W].

Opory przejmowania ciepła na powierzchni wewnętrznej i zewnętrznej danej przegrody, w zależności od kierunku przepływu strumienia cieplnego, odczytuje się z tablicy 7 normy [PN ISO 6946:2017]. 

 

Tabela 1. Opory przejmowania ciepła na powierzchni zgodnie z normą [3]

Opór przejmowania ciepła [(m2∙K)/W]	Kierunek strumienia ciepła
	w górę	poziomy	w dół
Rsi	0,10	0,13	0,17
Rse	0,04	0,04	0,04

                                                                                                          

Znając całkowity opór cieplny analizowanej przegrody, obliczamy jej współczynnik przenikania ciepła U [W/(m²∙K)] [3]: 

(2)

Opór cieplny przegrody, zawierającej w swojej budowie warstwy jednorodne i niejednorodne (np. ściana w konstrukcji szkieletu drewnianego), oblicza się metodą uproszczoną zgodnie z normą [3]. W metodzie tej dokonuje się myślowego podziału przegrody płaszczyznami adiabatycznymi (prostopadłymi do powierzchni przegrody) i izotermicznymi (równoległymi do powierzchni przegrody). W wyniku takiego podziału uzyskuje się tzw. kres górny (płaszczyzny adiabatyczne) oraz kres dolny (płaszczyzny izotermiczne) całkowitego oporu cieplnego, wyznaczanego zgodnie z poniższym wyrażeniem [3]:

(3)

gdzie:

• R_tot,upper -    kres górny całkowitego oporu cieplnego [m²∙K/W],
• R_tot;lower -    kres dolny całkowitego oporu cieplnego [m²∙K/W].

W wyniku zastosowania metody uproszczonej, analizowany komponent zostaje podzielony 
na warstwy i wycinki. Każdemu wycinkowi przegrody odpowiada względne pole powierzchni. Suma względnych pół powierzchni wszystkich wycinków komponentu jest równa jedności [3] 

(4) 

gdzie:

• f_a, f_b, …, f_q – względne pola powierzchni każdego wycinka danej przegrody [-].

Kres górny całkowitego oporu cieplnego (przy założeniu, że wszystkie płaszczyzny prostopadłe do powierzchni analizowanej przegrody są adiabatyczne) wyznacza się według poniższego wyrażenia [3]: 

(5)

gdzie:

• R_tot,a, R_tot,b, …, R_tot,q – całkowite opory cieplne każdego wycinka, [m²∙K/W].

Kres dolny całkowitego oporu cieplnego (przy założeniu, że wszystkie równoległe powierzchnie przegrody są izotermiczne) wyraża się następującym wzorem [3]:

(6)

Przy wyznaczaniu kresu dolnego, należy obliczyć równoważny opór cieplny Rj każdej warstwy niejednorodnej [3].

(7)

gdzie:

• R_aj, R_bj, …, R_qj – opory cieplne wycinków, budujących j-tą warstwę niejednorodną w danym komponencie [m²∙K/W].

Przy wyznaczaniu współczynnika przenikania ciepła przegrody wymagane jest uwzględnienie trzech poprawek, określonych w PN EN ISO 6946:2017 [3].  Wyróżnia się poprawkę z uwagi na:

• pustki powietrzne w warstwie izolacji,
• łączniki mechaniczne przebijające warstwę izolacyjną,
• zastosowanie dachu o odwróconym układzie warstw.

Poprawiony współczynnik przenikania ciepła, skorygowany o wyżej wymienione poprawki, oblicza się z następującego wzoru [3]: 

(8)

(9)

gdzie:

• ΔU_g    -    poprawka z uwagi na pustki powietrzne [W/(m²∙K)],
• ΔU_f    -    poprawka z uwagi na łączniki mechaniczne [W/(m²∙K)],
• ΔU_r    -    poprawka z uwagi na dach o odwróconym układzie warstw [W/(m²∙K)].

 

Poprawka z uwagi na pustki powietrzne
Zgodnie z normą, pustkami powietrznymi określa się przestrzenie powietrzne w izolacji termicznej przegrody lub między izolacją termiczną i przylegającą konstrukcją. Wyróżnia się dwie zasadnicze kategorie pustek powietrznych:

• szczeliny między arkuszami izolacyjnymi, płytami lub matami, lub między izolacją i elementami konstrukcji, w kierunku strumienia ciepła,
• wnęki w izolacji lub między izolacją i konstrukcją, prostopadle do kierunku strumienia ciepła.

Poprawkę ΔU_g wyznacza się z poniższego wzoru [3]: 

(10)

gdzie:

• R₁    -    opór cieplny warstwy zawierającej szczeliny [(m²∙K)/W],
• R_tot    -    całkowity opór cieplny komponentu z pominięciem mostków cieplnych [m²∙K/W],
• ΔU”    -    wartość przyjmowana zgodnie z tab. F.1 [3].  [W/(m²∙K)].

 

Tabela  2. Wartości czynnika ΔU’’ do wyznaczenia poprawki z uwagi na pustki powietrzne zgodnie z normą  PN ISO 6946:2017 [3]

Poziom	Opis	ΔU” [W/(m2∙K)]
0	Brak pustek powietrznych w obrębie izolacji lub gdy występują tylko mniejsze pustki powietrzne, które nie mają znaczącego efektu na współczynnik przenikania ciepła.	0,00
1	Pustki powietrzne przechodzące od ciepłej do zimnej strony izolacji, ale nie powodujące cyrkulacji powietrza między ciepłą i zimną stroną izolacji.	0,01
2	Pustki powietrzne przechodzące od ciepłej do zimnej strony izolacji, łącznie z wnękami powodującymi swobodną cyrkulację powietrza między ciepłą i zimną stroną izolacji.	0,04

Poprawka z uwagi na łączniki mechaniczne
Poprawkę do współczynnika U, z uwagi na łączniki mechaniczne, oblicza się jedną z dwóch procedur:

• obliczeniem szczegółowym,
• procedurą przybliżoną.

Wzór w obliczeniu szczegółowym jest następujący [3]: 

(11)

gdzie:

• n_f    -    liczba łączników na 1 m²,
• χ    -    punktowy współczynnik przenikania ciepła [W/K].

W procedurze przybliżonej poprawkę wyznacza się z poniższej zależności [3]:

(12) 

gdzie:

•     α = 0,8 (jeśli łącznik całkowicie przebija warstwę izolacji termicznej),
•     α = 0,8 d₁/d₀  (w przypadku łącznika wpuszczanego),
•     λ_f    -    współczynnik przewodzenia ciepła łącznika [W/(m∙K)],
•     A_f    -    pole przekroju poprzecznego jednego łącznika [m²],
•     d₀    -    grubość warstwy izolacji zawierającej łącznik [m],
•     d₁    -    długość łącznika, który przebija warstwę izolacyjną [m],
•     R₁    -    opór cieplny warstwy izolacji przebijanej przez łączniki [(m²∙K)/W],
•     R_tot  -    całkowity opór cieplny komponentu z pominięciem jakichkolwiek mostków cieplnych [m²∙K/W].     

 

Poprawka z uwagi na dach o odwróconym układzie warstw

Poprawkę, wynikającą z przepływu wody między izolacją i membraną wodochronną, określa się z następującej zależności [3]: 

(13)

gdzie:

• p    -    średnia wartość opadów atmosferycznych podczas sezonu ogrzewczego, na podstawie danych odpowiednich dla lokalizacji lub podana przez przepisy lokalne, regionalne czy krajowe lub inne dokumenty krajowe czy normy [mm/dzień],
• f    -    czynnik deszczowy podający frakcję p dochodzącą do membrany wodochronnej [-],
• x    -    czynnik zwiększenia strat ciepła spowodowanych przez wodę deszczową wpływającą na membranę [W∙dzień/(m²∙K∙mm)],
• R₁    -    opór cieplny warstwy izolacji powyżej membrany wodochronnej [m²∙K/W],
• R_tot    -    całkowity opór cieplny konstrukcji przed zastosowaniem poprawki [m²∙K/W].