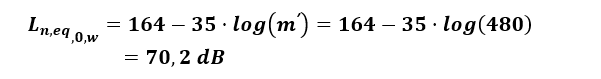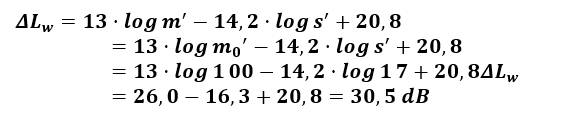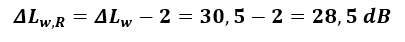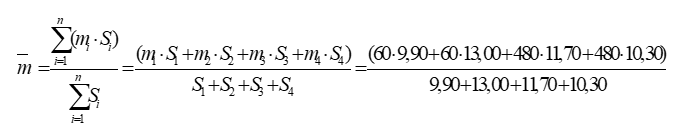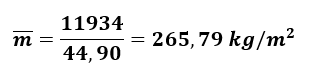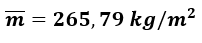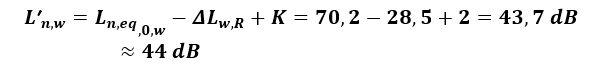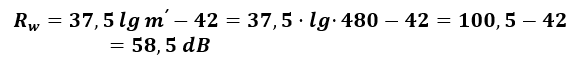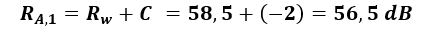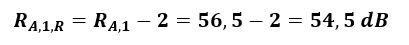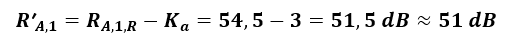Określenie wskaźników oceny przybliżonej izolacyjności od dźwięków powietrznych i uderzeniowych

Przybliżoną izolacyjność od dźwięków powietrznych jak i uderzeniowych między pomieszczeniami rozdzielonymi stropem można określić za pomocą pomiarów terenowych [10]  jeżeli budynek istnieje. Zrobienie tego na etapie projektowania budynku jest niemożliwe z oczywistych względów. W związku z powyższym w takim przypadku konieczne jest użycie metod teoretycznych polegających na przeprowadzeniu odpowiednich obliczeń uwzględniających drogi pośrednie przenoszenia dźwięku:

• dla dźwięków powietrznych wg PN-EN 12354 – 1:2017-10 [7],  podane zostały metody wykonania takich obliczeń umożliwiających uzyskanie wyników dotyczących zarówno wartości R’ w poszczególnych pasmach częstotliwości (wg metody dokładnej) jak i jednoliczbowych wartości wskaźników R’_A,1 lub D_n,T,A,1 (wg metody uproszczonej),
• jednoliczbowych wartości wskaźników R’_A,1 (wg metody szacunkowej) wg [17], 

• dla dźwięków uderzeniowych wg PN-EN 12354 – 2:2017-10 [8],  podane zostały metody wykonania takich obliczeń umożliwiających uzyskanie wyników dotyczących zarówno wartości L’n w poszczególnych pasmach częstotliwości (wg metody dokładnej) jak i jednoliczbowych wartości wskaźników L’_n,w  (wg metody uproszczonej),
• jednoliczbowych wartości wskaźników L’_n,w  (wg metody uproszczonej) wg [15]. 

Powyższe metody teoretyczne określenia przybliżonej izolacyjności przedstawiono wcześniej w części dotyczącej izolacyjności przybliżonej od dźwięków powietrznych  oraz izolacyjności przybliżonej od dźwięków uderzeniowych.  Ze względu na liczbę potrzebnych danych oraz pracochłonność obliczeń, możliwość wykorzystania metody „dokładnej” oraz „uproszczonej” zarówno do określenia izolacyjności od dźwięków powietrznych jak i uderzeniowych wg normy [7]  i [8],  przez projektantów wydaje się mocno ograniczona. Metoda „szacunkowa” pomimo, że obarczona wieloma ograniczeniami może okazać się pomocna dla większości „standardowych” sytuacji projektowych. 

W związku z powyższym poniżej przedstawiono przykłady obliczeniowe dotyczące metody „szacunkowej”. 

Ponadto zachęcamy do skorzystania z tabel doboru systemów podłogowych ze względu na izolacyjność akustyczną przegród i wytrzymałość posadzki [Floor-Matrix ], które zawierają gotowe rozwiązania systemowych podłóg pływających dobranych tak,  aby spełnić wymagania normowe. Tablice doboru systemu uwzględniają rodzaj konstrukcji zarówno stropu jak i przegród pionowych w budynku.

Przykład nr  1
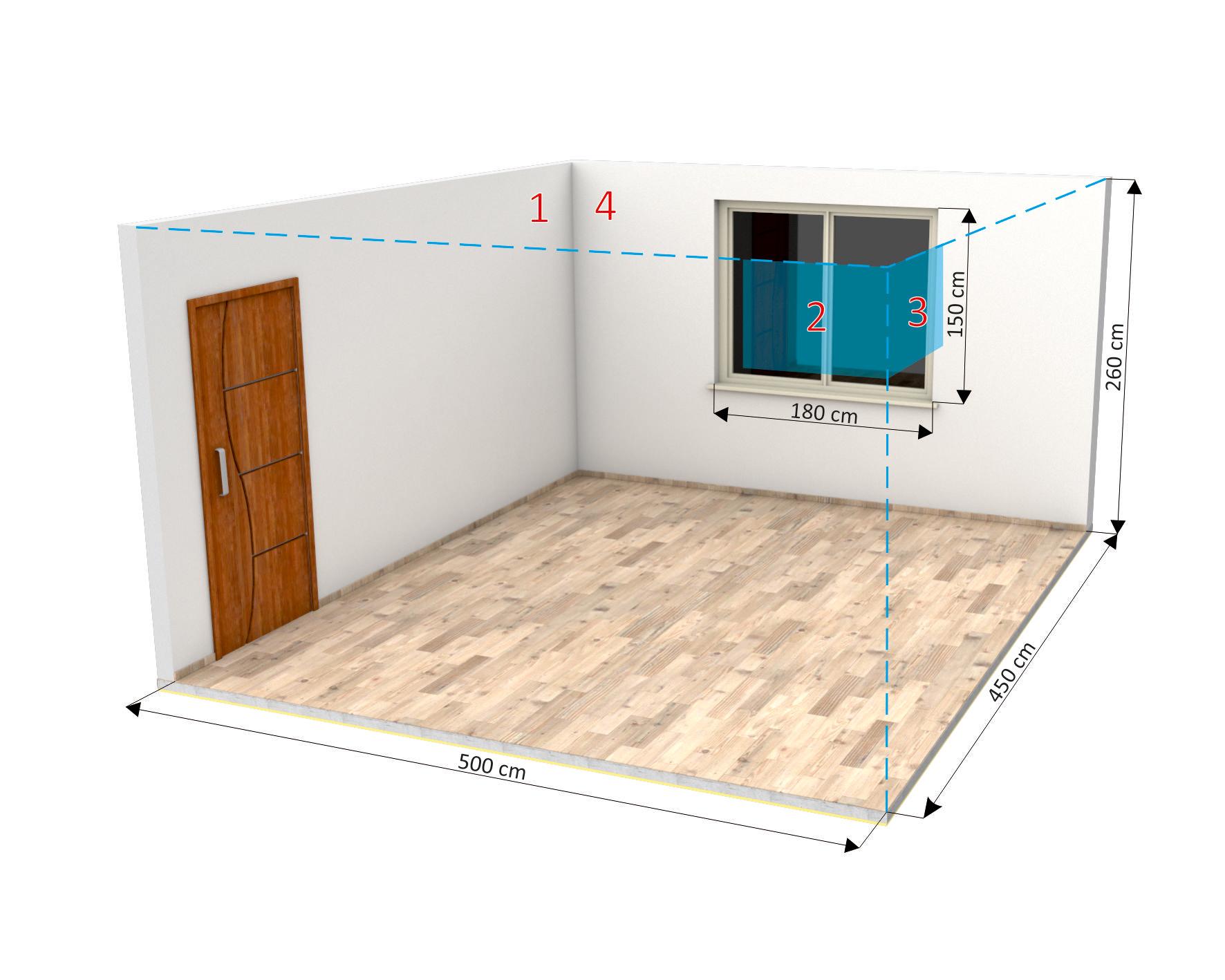
Sprawdzić czy rozwiązanie projektowe przedstawione na rysunku spełnia wymagania normowe [6]  pod względem ograniczenia dźwięków uderzeniowych. Sytuacja dotyczy rozdzielenia stropem pomieszczeń mieszkalnych w budynku wielorodzinnym.

Rys. 1. Widok pomieszczenia w budynku mieszkalnym wielorodzinnym z widoczną numeracją przegród bocznych 1÷4 uwzględnionych w obliczeniach.

Dane:

• wysokość użytkowa mieszkania h = 260 cm,
• ściana boczna (działowa) „1”i „2” - murowana z bloczków z betonu komórkowego gr. 10 cm, (masa powierzchniowa ściany bez tynku 60 kg/m²), obustronnie tynk cem.-wap. gr. 12 mm),
• ściana wewnętrzna (międzymieszkaniowa) „3” – żelbetowa gr. 20 cm, (masa powierzchniowa ściany bez tynku 480 kg/m²), obustronnie tynk cem.-wap. gr. 12 mm.,
• ściana zewnętrzna „4” -żelbetowa gr. 20 cm, (masa powierzchniowa ściany bez tynku 480 kg/m²), jednostronnie tynk cem.-wap. gr. 12 mm., jednostronnie ocieplenie w postaci systemu w technologii lekkiej mokrej,
• otwór drzwiowy 90/200 w ścianie „1”,
• otwór okienny 150/180 w ścianie „4”,
• strop żelbetowy gr. 20 cm, masa powierzchniowa 480 kg/m² + podłoga pływająca (wełna mineralna szklana Isover TDPT 2 cm, sztywność dynamiczna s’=14 MN/m3 [19] + jastrych cementowy 5 cm.

Przyjęto:

• graniczną maksymalną wartość wskaźnika przybliżonego poziomu uderzeniowego dla stropu L’n,w ≤ 55 dB (wg. tab. 9 wiersz I.1. kolumna 4),
  m1 = m2 = 60 kg/m2,
  m3 = 480 kg/m2,
  m4 = 480 kg/m2,
  m‘ = 480 kg/m2 – masa powierzchniowa stropu bez warstw dodatkowych,
  m‘ = 100 kg/m2 – masa powierzchniowa warstwy dociskowej podłogi pływającej (ze względu na kolizję oznaczeń wynikającą z wzorów (4) części opisującej izolacyjność akustyczną   i (4) części opisjącej izolacyjność przybliżoną od dźwięków uderzeniowych  w dalszych obliczeniach przyjęto m0‘ = 100 kg/m2).

Obliczono:

• S_drzwi = 0,90 2,00 = 1,80 m² – powierzchnia otworu drzwiowego,
• S₁ = 4,50 2,60 – 1,80 = 11,70 – 1,80 = 9,90 m² – powierzchnia ściany „1” po odliczeniu powierzchni otworu drzwiowego,
• S₂ = 5,00 2,60 = 13,00 m² – powierzchnia ściany „2”,
• S₃ = 4,50 2,60 = 11,70 m² – powierzchnia ściany „3”,
• S_okna = 1,80 1,50 = 2,70 m² – powierzchnia otworu okiennego,
• S₄ = 5,00 2,60 – 2,70 = 13,00 – 2,70 = 10,30 m² – powierzchnia ściany „4” po odliczeniu powierzchni otworu okiennego.

W związku z brakiem danych pomiarowych pochodzących z laboratorium dotyczących izolacyjności od dźwięków uderzeniowych „gołego” stropu posłużono się worem (4)  i obliczono wartość równoważnego ważonego wskaźnika poziomu uderzeniowego znormalizowanego dla stropu bez dodatkowych warstw.

W związku z brakiem danych pomiarowych pochodzących z laboratorium dotyczących izolacyjności od dźwięków uderzeniowych podłogi pływającej posłużono się wzorem obliczeniowym (4)  i obliczono wartość ważonego wskaźnika zmniejszenia poziomu uderzeniowego przez podłogę ΔL_w.

Z wzoru (2)  obliczono wartość projektowego ważonego wskaźnika zmniejszenia poziomu uderzeniowego przez podłogę ΔL_w,R.

Z wzoru (3)  obliczono średnią masę powierzchniową przegród bocznych (ścian działowych i ściany zewnętrznej):

Na podstawie m'=480 kg/m² i obliczonej wartości

wyznaczono poprawkę:
K = 2 dB (na podst. tablicy 1).
 

Z wzoru (1)  obliczono wartość wskaźnika ważonego przybliżonego poziomu uderzeniowego znormalizowanego L’_n,w.

Odp. Przybliżona izolacyjność od dźwięków uderzeniowych dla stropu z podłogą, rozdzielającego mieszkania wyrażona wartością wskaźnika L’_n,w wyniosła 44 dB. Tym samym ograniczenie górne określone wskaźnikiem L’_n,w ≤ 55 dB należy uznać za spełnione.

Przykład nr 2
Sprawdzić czy rozwiązanie projektowe z przykładu 1 spełnia wymagania normowe [6] pod względem ograniczenia dźwięków powietrznych.

Dane:

• przyjęto jak w przykładzie 1.

Przyjęto:

• wymaganą minimalna izolacyjność od dźwięków powietrznych dla stropu R’A,1 ≥ 51 dB (wg. tab. 3 wiersz I.1. kolumna 4) 
• poprawkę K_a = 3 dB (na podst. tablicy II.1-1.1. wiersz 4.1. Instrukcji ITB nr 406/2005 [17]) 

Obliczono:

W związku z brakiem danych pomiarowych pochodzących z laboratorium posłużono się worami obliczeniowymi (1),  (2),  (3). 

Z wzoru (1) obliczono:

Na podstawie (2)  przyjęto wartość wskaźnika C = - 2 dB (jest to wariant bardziej krytyczny względem C = - 1 dB).
Z wzoru (3)  obliczono:

Z wzoru (2)  obliczono:

Z wzoru (1)  obliczono:

Odp. Przybliżona izolacyjność akustyczna właściwa pomiędzy mieszkaniami przez strop wyrażona wartością wskaźnika R’_A,1 wyniosła 51 dB. Tym samym wymagane minimum określone wskaźnikiem R’_A,1 ≥ 51 dB należy uznać za spełnione.

Konkluzja!

Obliczenia nie uwzględniają pozytywnego wpływu podłogi pływającej na izolacyjność od dźwięków powietrznych pomiędzy pomieszczeniami. W zakresie izolacyjności od dźwięków powietrznych wpływ podłogi ma mniejsze znaczenie niż w przypadku dźwięków uderzeniowych. Na podstawie wyników badań laboratoryjnych przedstawionych w instrukcji [18]  wzrost wskaźnika R_A,1 na skutek zastosowania na „gołym” stropie podłogi pływającej ocenić można na ΔR_A,1 = 2÷5 dB. Rzeczywisty wzrost wskaźnika uzależniony jest nie tylko od rodzaju podłogi pływającej (masy powierzchniowej warstwy dociskowej oraz sztywności dynamicznej warstwy sprężystej) ale także od parametrów „gołego” stropu (im wyższa izolacyjność „gołego” stropu tym mniejszy wzrost wskaźnika R_A,1 na skutek zastosowania podłogi pływającej). W przypadku konieczności obliczeniowego uwzględnienia wpływu podłogi pływającej na izolacyjność stropu, można posłużyć się w tym celu metodyką wg normy [7].  Wyniki pomiarów wskazują jednak na nieco niższe wartości wskaźnika poprawy izolacyjności akustycznej właściwej ΔR_A,1 niż wynikające z obliczeń na podstawie [7]. 

Stropy o konstrukcji drewnianej 
W przypadku stropów o konstrukcji drewnianej nie ma możliwości określenia ich parametrów dźwiękoizolacyjnych w inny sposób jak tylko za pośrednictwem pomiarów laboratoryjnych. Programy komputerowe wykorzystujące metody teoretyczne prognozowania izolacyjności od dźwięków powietrznych jak i uderzeniowych, bazujące na zależności „prawa masy” nie pozwalają na określenie parametrów dźwiękoizolacyjnych z wystarczającą dokładnością dla tego rodzaju konstrukcji. W tej sytuacji projektant w celu prawidłowego doboru stropu, zmuszony jest korzystać z gotowych rozwiązań stropów drewnianych, przebadanych wcześniej w laboratorium. Również ograniczenia związane ze stosowaniem modeli normowych [7], [8] służących do „przejścia” z wartości w laboratorium (R_A,1, Ln,w) na wartości w budynku (R’_A,1, L’_n,w) w przypadku stropów drewnianych w znaczący sposób ograniczają możliwość stosowania tychże modeli. 

W związku z powyższym w części przedstawiającej rozwiązania z wełną mineralną ISOVER   pokazano przykładowe rozwiązania stropów drewnianych. 

Stropy jednorodne
W przypadku stropów o konstrukcji traktowanej przez normy [7] i [8]  jako jednorodne istnieją możliwości określenia ich parametrów dźwiękoizolacyjnych za pomocą obliczeń teoretycznych. Z możliwości tej można korzystać wówczas kiedy nie dysonujemy wynikami pomiarów laboratoryjnych. Zawsze pamiętać należy, że wyniki pomiarów laboratoryjnych najlepiej odzwierciedlają rzeczywiste parametry dźwiękoizolacyjne przegrody. Możliwości prognozy parametrów dźwiękoizolacyjnych dla stropów o konstrukcji „jednorodnej” przedstawiono w części opisującej izolacyjność akustyczną.   

W celu „przejścia” z wartości w laboratorium (R_A,1, L_n,w) na wartości w budynku (R’_A,1, L’_n,w) w przypadku stropów „jednorodnych” należy stosować modele normowe [7], [8]  opisane w częściach dotyczących izolacyjności przybliżonej od dźwięków powietrznych   i izolacyjności przybliżonej od dźwięków uderzeniowych . Sposób postępowania przedstawiono w przykładzie obliczeniowym nr 1 i 2.  Wartości wskaźników oceny izolacyjności od dźwięków powietrznych i uderzeniowych dla przykładowych stropów o budowie „jednorodnej” zestawiono w tablicy nr 1.

* - wartości wskaźników obliczone za pomocą wzorów (1)÷(4)

Na podstawie porównania wyników dla stropu żelbetowego pełnego gr. 14 cm (tablica 1 wiersz 8 i 9), można stwierdzić, że wartości wskaźników R_w,R, R_A,1,R i R_A,2,R (wiersz 9÷16) obliczone wg metodyki przedstawionej w PN-EN 12354-1:2002 [15]  dają wartości niższe, więc parametry „gorsze” od wyznaczonych w badaniach laboratoryjnych o ok. 2 dB. W przypadku wskaźnika L_n,eq,0,w sytuacja jest odmienna. Wartości otrzymane na podstawie obliczeń są niższe o ok. 1,5 dB od wartości wyznaczonych w badaniach laboratoryjnych co z kolei oznacza, że parametry obliczone są „lepsze” od tych wyznaczonych w laboratorium. Wniosków tych nie należy uogólniać na wszystkie rodzaje stropów „jednorodnych”.